|
 sayısına ait değerin, gittikçe daha fazla basamağını hesaplama
tutkusunun yanısıra, matematikçilerin rüyalarına giren başka bir
sayısına ait değerin, gittikçe daha fazla basamağını hesaplama
tutkusunun yanısıra, matematikçilerin rüyalarına giren başka bir
 problemi de, daireyi kare yapma problemiydi. Bu uğraşıya, kendilerini kaptıranların önderi Anaksagoras'tır (M.Ö. 500-428) Bir ara Atina'da,
zındıklıkla suçlanıp hapse atılan Anaksagoras, burada can sıkıntısından, daireyi kare
yapmanın yollarını aramaya başlar. Kendisinin çözdüğünü sandığı, bazı yaklaşık sonuçlar elde edler. Daha sonra,
Kilyos'lu Hippokrates (M.Ö. 5. yüzyıllın ikinci yarısı) , aşağıdaki şekilde problemi de, daireyi kare yapma problemiydi. Bu uğraşıya, kendilerini kaptıranların önderi Anaksagoras'tır (M.Ö. 500-428) Bir ara Atina'da,
zındıklıkla suçlanıp hapse atılan Anaksagoras, burada can sıkıntısından, daireyi kare
yapmanın yollarını aramaya başlar. Kendisinin çözdüğünü sandığı, bazı yaklaşık sonuçlar elde edler. Daha sonra,
Kilyos'lu Hippokrates (M.Ö. 5. yüzyıllın ikinci yarısı) , aşağıdaki şekilde
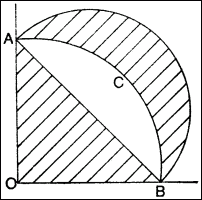 taranmış
ACBA alanının, AOB üçgenin alanına eşit olduğunu gösterir Buna benzer başka örnekler gösterir ki, belli eğrilerle sınırlanmış, bazı bölgelerin alanlarına eşit alanda kareler çizilebilir. taranmış
ACBA alanının, AOB üçgenin alanına eşit olduğunu gösterir Buna benzer başka örnekler gösterir ki, belli eğrilerle sınırlanmış, bazı bölgelerin alanlarına eşit alanda kareler çizilebilir.
18. yüzyılın sonlarından başlayarak, dairenin kare yapılmasının imkansız
olduğu fikri, matematikçilere hakim oldu. Bu kuşku o kadar büyük ki, 1775 te, Paris Bilimler Akademisi, devr-i daim makinesi
projeleri, açıyı pergel ve cetvel kullanarak üç eşit parçaya bölme yöntemlerinin
yanısıra daireyi kare yapma yöntemlerini de, artık inceleme
kararı aldı.
1775 te Euler, 1794 te Legendra,
 nin belki de, cebirsel bir sayı
olmadığına, üstel bir sayı olması gerektiğine ilişkin inançlarını
belirtirler. Fakat nin belki de, cebirsel bir sayı
olmadığına, üstel bir sayı olması gerektiğine ilişkin inançlarını
belirtirler. Fakat  nin üstel olduğunun kanıtlanması için, 100 yıl beklendi.
Sonunda, 1882 yılında, Alman matematikçi Lindermann,
nin üstel olduğunun kanıtlanması için, 100 yıl beklendi.
Sonunda, 1882 yılında, Alman matematikçi Lindermann,  nin üstel olduğunu ispatladı.
nin üstel olduğunu ispatladı.
|
|
|
|